Trigonometry question...

[OldFrog75]

I'm trying to compute the distance to a waypoint for a 1 degree change in heading off the wind.

I know 1 degree off course translates to 1 mile off course for every 60 miles sailed. I also know that a boat trying to sail to a waypoint directly into the wind with only one tack will sail a course more or less resembling an isosceles triangle.

My question is: how does one determine the length of the two legs given different degrees off the wind, which when added together will give total distance sailed.

I could figure it out with a nav chart and a protractor but knowing the mathematical formula could be easier and faster (or knowing the formula to program into a computer spreadsheet).

As a practical example, how much further does a boat which can point no higher than 60 degrees off True wind sail to a waypoint compared to one that can sail 30 degrees off True wind?

I've been estimating it as (100' feet/degree/mile) X 2 as compared to a perfect 45, 45, 90 isosceles triangle but I'm thinking that might be way off.

[ksanders]

instead of explaining it, since the numbers will not necessarily work for your exact situation I'll show yoy how to learn it yourself.

On a piece of paper draw a straight line representing a straight course between your origin and your destination.

Then draw a line at whatever angle off course you are required to travel in your conditions. The length will be the miles you travel before you change course to tack back

Now using the line you just drew, draw another line to the closest point you can along your intended route.

See the triangle??? it is a right triangle and the length of your original course is the hypotonuse of that triangle.

So, take the take the distance you traveled and multiply it by the cos of the course deviation you had to folllow in degrees. The result will be the distance you traveled, measured on your original intended course towards your destination.

Then take 90 minus the course deviation and multiply your distance traveled by the cos of that number. The result is the distance you are actually off course.

Now you can set your tack back and form a new triangle.

[Stu Jackson]

Trigonometry - Wikipedia, the free encyclopedia

[svGenesis]

90 feet per degree for every mile of distance.

[OldFrog75]

Originally Posted by Stu Jackson

Trigonometry - Wikipedia, the free encyclopedia

I read it. Little beyond my comprehension. Was hoping for something simple for determining the lengths of the sides of an isosceles triangle given the length of the base and angles of the legs off the base...

[StuM]

In that special case, you can do it in your head.
Draw the triangles for just the first half.
In a 30°-60°-90° triangle the sides are in the ratio 1 : 2 : .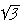

So
At 30° you sail 2 for every 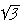(1.732) forward. (i.e 1.155 for every 1 forward)
At 60° you sail 2 for every 1 forward.

So to answer your question, you sail an extra 0.846 NM for every mile ahead at 60° compared to 30°.


The general rule is the distance sailed to make 1 unit to windward is 1/cos(angle)

cos(30°) = 0.866 so the distance is 1/0.866 = 1.155
cos(45°) = 0.707 so the distance is 1/0.707 = 1.414
cos(60°) = 0.5 so the distance is 1/0.5 = 2

Beyond 60°, it gets worse fast!
65° = 2.37
70 °= 2.93
75° = 3.86

[fryewe]

The answer to your practical example is that a sailboat that can sail 30 degrees off the wind that is sailing a rhumb line to a destination directly upwind will have to sail about 1.15 nm for each nm of rhumb line route (1/cos 30=1/0.866=1.15), and a sailboat sailing 60 degrees off the wind to that same destination will sail 2 nm for each mile of route (1/cos 60=1/0.5=2).

The relationship is nonlinear, a function of the cosine of the angle being sailed off track. It's easily calculated in the manner shown in the example. Since the calculation will be an estimate of the distance to be traveled due to leeway and other effects, it might be useful to your needs to make up a simple table of 1/cos values at 5 degree intervals from about 40 to 60 degrees off track, and multiply times the distance to waypoint or destination.

Such a table would be: 1/cos 40=1.30
1/cos 45=1.41
1/cos 50=1.56
1/cos 55=1.74
1/cos 60=2.00

...and the values can be rounded for ease of mental estimation if needed, eg, 1.3, 1.4, 1.55, 1.75, 2...or coarser if desired.
.

[StuM]

Originally Posted by rip-omatic

90 feet per degree for every mile of distance.

So If I sail 90° to my course, that would be 8,100 feet sailed to make a mile?
How about if I sail more than 90° to my course?

[andres]

I am not sure if I undestand you correctly, but call L de distance between you and your destination, call alpha the angle off course you are sailing, and call A the distance you sail in one tack. I suppose you do only two tacks with the same angle of course in each tack, so you have an isosceles triangle where two sides have lenght A, one side lenght L and the measure of each of the two equal angles is alpha. If you cut in half this triangle with a perpendicular line to the line between the origin and your destination pasing trough the other vertex (the point where you change tacks), then you have a rectangular triangle where the hypotenuse is A, and the leg adjacent to angle alpha is L/2. Then the cosine of alpha is cos(alpha)=L/(2A), and hence the total distance you sail with the two tacks is 2A=L/cos(alpha).

Let us now consider your example. If you sail at a tacking angle of 60 degrees, then cos(60º)=1/2 and then L/cos(alpha)=2L, but if you sail at 30 degrees, then you get cos(30º)=0,87 and then L/cos(alpha)=1,15 L. That is if your destination is at 100 miles and your tacking angle is 60º, then you need to sail 200 miles, but if yor tacking angle is 30º, then you only need to sail 115 miles.

I hope this answer your question.

[dougdaniel]

If you want to program a spreadsheet, the answer is the straight line distance divided by the cosine of the angle off the wind. Notice that most spreadsheet do angles in radians. remember that 360 degrees is equal to two pi radians. Rather than enter pi as 3.14159, you might use the function pi() that most spreadsheets use. For example, if the angle was 45% then the angle would be pi/4 radians.

If you are using Excel, then this formula will work: =L8/(COS(2*PI()/L7)). Here I put the straight line distance in L8 and the angle off the wind in L7. The angle is entered in degrees.

[captain58sailin]

Bowditch has some very helpful tables for this question. Those who are conversant with Excel or similar program can enter the formulas into a cell and then simply enter the relevant data to obtain the desired answer.

[OldFrog75]

Thanks to everyone who responded. Lots of good information and suggestions. I think you've given me enough help to get what I need.

[OldFrog75]

Originally Posted by dougdaniel

If you are using Excel, then this formula will work: =L8/(COS(2*PI()/L7)). Here I put the straight line distance in L8 and the angle off the wind in L7. The angle is entered in degrees.

What goes inside the parentheses for PI()? Didn't quite understand that.

[Seaworthy Lass]

Originally Posted by OldFrog75

What goes inside the parentheses for PI()? Didn't quite understand that.

Nothing, if you enter PI() then the value for pi is inserted.

[Seaworthy Lass]

Originally Posted by dougdaniel

If you are using Excel, then this formula will work: =L8/(COS(2*PI()/L7)). Here I put the straight line distance in L8 and the angle off the wind in L7. The angle is entered in degrees.

If you are entering radians, not degrees into cos, don't you mean the distance travelled tacking =L8/(COS(2*PI()*L7/360))
Where L7 is the angle off the true wind in degrees.

OldFrog, if you are using a calculator, it may have a cos button. Just check 'deg' is written in tiny writing in the corner of the screen (if not, press the deg/rad button), enter the angle off the true wind and hit 'cos'.

All you need to do is divide the actual straight line distance by this figure and you have the distance travelled tacking .

SWL